- ...sciel
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
- Supported in part by the Polish
Research Council grant KBN 2 P03B 073 15. E-mail:
chrusciel@univ-tours.fr
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Nagy
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
-
Supported by a grant from Région Centre. E-mail:
nagy@gargan.math.univ-tours.fr
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
satisfy
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
- The summation convention is used throughout. We use
Greek indices for coordinate components and lower-case Latin
indices for the tetrad ones; upper-case Latin indices run from
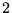 to
to 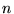 and are associated either to coordinates or to frames on
and are associated either to coordinates or to frames on
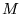 , in a way which should be obvious from the context. Finally
Greek bracketed indices
, in a way which should be obvious from the context. Finally
Greek bracketed indices 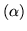 etc. refer to
objects defined outside of space-time, such as the Killing algebra
etc. refer to
objects defined outside of space-time, such as the Killing algebra
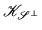 , or an exterior embedding space, and are also summed
over.
, or an exterior embedding space, and are also summed
over.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
- The integral over
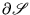 should be understood
by a limiting process, as the limit as
should be understood
by a limiting process, as the limit as 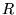 tends to infinity of
integrals over the sets
tends to infinity of
integrals over the sets 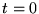 ,
, 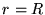 .
.
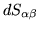 is defined
as
is defined
as
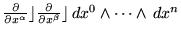 , with
, with 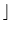 denoting contraction;
denoting contraction; 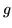 stands
for the space-time metric unless explicitly indicated otherwise.
Square brackets denote antisymmetrization with an appropriate
numerical factor (
stands
for the space-time metric unless explicitly indicated otherwise.
Square brackets denote antisymmetrization with an appropriate
numerical factor (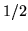 for two indices), and
for two indices), and
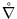 denotes
covariant differentiation with respect to the background metric
denotes
covariant differentiation with respect to the background metric
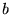 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scalar
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
- Related results under
less restrictive conditions can be found in [13].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... invariant
![[*]](file:/usr/local/lib/latex2html/icons/footnote.png)
- If the
scalar curvature of
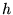 vanishes, then Einstein equations require the
constant
vanishes, then Einstein equations require the
constant 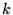 in the metric to vanish. In that case there arises an
ambiguity in the definition of mass related to the possibility of
rescaling
in the metric to vanish. In that case there arises an
ambiguity in the definition of mass related to the possibility of
rescaling 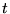 and
and 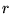 without changing the form of the metric, which
rescales the mass. (This freedom does not occur when
without changing the form of the metric, which
rescales the mass. (This freedom does not occur when 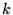 is non-zero.)
This ambiguity can be removed by arbitrarily choosing some
normalization for the
is non-zero.)
This ambiguity can be removed by arbitrarily choosing some
normalization for the 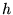 -volume of
-volume of 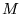 , e.g.
, e.g. 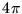 in
dimension
in
dimension 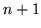 =4.
=4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.